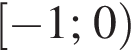Корень уравнения
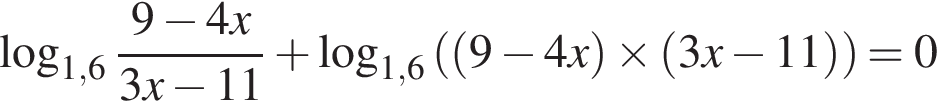
(или сумма корней, если их несколько) принадлежит промежутку:
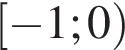
Корень уравнения
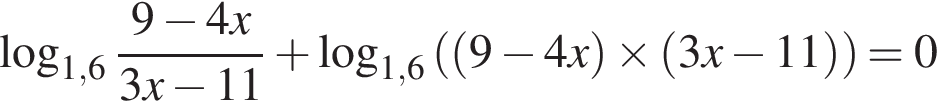
(или сумма корней, если их несколько) принадлежит промежутку:
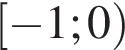
Корень уравнения
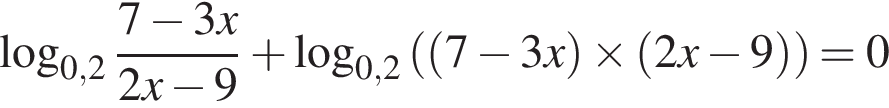
(или сумма корней, если их несколько) принадлежит промежутку:
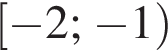
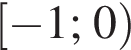
Корень уравнения
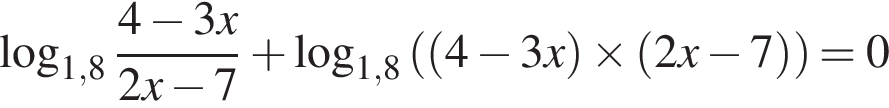
(или сумма корней, если их несколько) принадлежит промежутку:
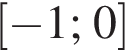
Корень уравнения
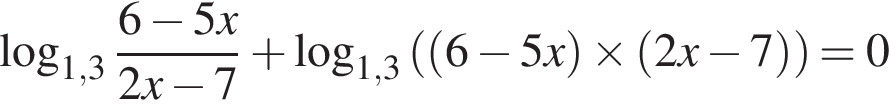
(или сумма корней, если их несколько) принадлежит промежутку:
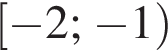
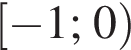
Корень уравнения
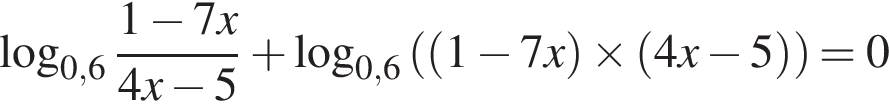
(или сумма корней, если их несколько) принадлежит промежутку: